アンケートで不正回答を防ぐことは難しい？不正回答者の傾向を徹底分析

回答時間が短い人は不正回答者の傾向が高い
不正回答者の予測の精度を確認する
- ROC曲線で確認
- PR曲線で確認
まとめ

回答時間が短い人は不正回答者の傾向が高い

Satisficing回答者の予測に関する実験調査結果の続きです。最後に、少し蛇足になりますが、予測の検証をしてみました。
今回の記事では、前回記事のロジスティック回帰分析による予測を、ステップワイズ法により変数整理した予測モデルにしてご紹介します。

予測モデル（ロジスティック回帰）

標準化係数を見ると、一番Satisficing回答者の予測に影響しているのは「回答時間（対数）」（マイナスの方向に影響）、次いで「ストレートライナー」となっています。

不正回答者の予測の精度を確認する

では、この予測モデルで、残しておいた900人の検証用サンプルを予測してみます。

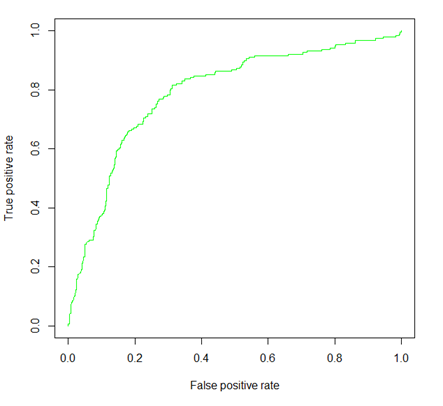
ROC曲線で確認

ROC曲線(AUC=0.789)

上図はROC曲線といわれるもので、予測の精度を確認するのに使われます。

横軸のFalse Positive rate(FP)は、実際はSatisficing回答者でないのに、Satisficing回答者だと予測してしまう比率です。コロナ禍でだいぶ人口に膾炙した、いわゆる「疑陽性」率になります。
縦軸のTrue Positive rate(TP)は、Satisficing回答者のうち、正しく予測できた比率です。

予測モデルからは予測値が0～1のスコアとして算出されますから、このスコアのどこを判別の閾値（カットオフ値）とするかで、上記の比率は変化します。この変化の様子をみるのが図中緑色のROC曲線になります。

図の左下隅は、カットオフ値が0、つまり誰もSatisficing回答者と判別しない場合です。この場合、FPもTPも0になるのはわかると思います。また、右上隅はカットオフ値=1、全ての人をSatisficing回答者と判別する場合で、この場合はFPもTPも1（100％）になります。
図の枠（四角形）の中に占めるROC曲線の下の面積をAUC(Area Under Curve)といい、これを予測精度の指標（0.5～１の値をとる）とします。つまり、右上から左下への対角線からみて上にふくらんだ曲線になっているほどよい予測というわけです。

今回の結果ではAUC=0.789で中程度の良さの予測といえ、予測モデルの改善余地はまだありそうです。

さて、0と1の間のどこかに適切なカットオフ値があるはずですが、まずカットオフ値=0.5として、予測結果と実際のクロス集計をとってみます。こうしたクロス集計を混同行列と呼びます。

混同行列（カットオフ値=0.5）

検証用サンプル900人のうち、Ｓ（Satisficing）回答者は189人いたのですが、カットオフ値0.5ではそのうち正しく予測できたのは57人でした。また、非S回答者のうち53人をS回答者と誤って予測しています。

カットオフ値の決定方法にはいろいろあるのですが、一番わかりやすいのは上記混同行列の黄色の部分、つまり正しく判別できた人数（正判別率といいます）を最大にするものだとおもいます。

しかし、今回もそうですが（S回答者の比率は全体の2割強）、予測する対象の割合に偏りがある（たいてい少ない）場合、この方法が一番良い予測にはならないことがあります。

正判別率を最大にする方法だと、今回の予測ではカットオフ値は0.537，混同行列は以下のようになります。

混同行列（正判別率最大、カットオフ値=0.537）

カットオフ値決定にはこのほか、Youdenの指標、F値を最大にする方法などがあります。

Youdenの指標は、ROC曲線と対角線の距離が最大になる点をとるものです。

F値は、適合率と再現率の調和平均をいいます。適合率(precision)は、TP/(TP+FP)、つまりSatisficing回答者と予測したうち実際そうだった人の割合で、予測の精度ともいえます。再現率(recall)は、ROC曲線のTrue Positive rateと同じで、TP/(TP+FN)、つまり、実際のSatisficing回答者のうち、何人正しく予測できたかの割合で、予測の捕捉率ともいえます。

また、この適合率を縦軸、再現率を横軸にとったグラフを、PR曲線といいます。